You Must Know the Mean of an Activity in Order to Determine Its Standard Deviation
Detached Random Variables
Mean or Expected Value and Standard Deviation
The expected value is ofttimes referred to as the "long-term" average or mean. This means that over the long term of doing an experiment over and over, you would await this average.
You toss a coin and tape the result. What is the probability that the event is heads? If yous flip a coin two times, does probability tell you that these flips will issue in one heads and one tail? You lot might toss a off-white coin ten times and record ix heads. Equally you lot learned in (Effigy), probability does not draw the short-term results of an experiment. It gives information about what tin can be expected in the long term. To demonstrate this, Karl Pearson in one case tossed a fair money 24,000 times! He recorded the results of each toss, obtaining heads 12,012 times. In his experiment, Pearson illustrated the Law of Large Numbers.
The Law of Large Numbers states that, as the number of trials in a probability experiment increases, the difference between the theoretical probability of an event and the relative frequency approaches nothing (the theoretical probability and the relative frequency get closer and closer together). When evaluating the long-term results of statistical experiments, we often want to know the "average" outcome. This "long-term average" is known as the mean or expected value of the experiment and is denoted by the Greek alphabetic character μ. In other words, after conducting many trials of an experiment, y'all would expect this average value.
NOTE
To find the expected value or long term average, μ, simply multiply each value of the random variable by its probability and add the products.
A men'southward soccer team plays soccer null, ane, or two days a week. The probability that they play zero days is 0.2, the probability that they play one day is 0.5, and the probability that they play two days is 0.three. Discover the long-term average or expected value, μ, of the number of days per week the men's soccer squad plays soccer.
To practice the trouble, first allow the random variable X = the number of days the men's soccer squad plays soccer per week. 10 takes on the values 0, 1, two. Construct a PDF table adding a cavalcade x*P(ten). In this column, yous will multiply each x value by its probability.
| x | P(x) | x*P(x) |
|---|---|---|
| 0 | 0.ii | (0)(0.two) = 0 |
| one | 0.five | (1)(0.v) = 0.5 |
| 2 | 0.3 | (2)(0.3) = 0.vi |
Add the last column ten*P(x) to find the long term average or expected value: (0)(0.2) + (one)(0.five) + (2)(0.iii) = 0 + 0.five + 0.6 = 1.one.
The expected value is 1.1. The men'south soccer team would, on the boilerplate, expect to play soccer ane.1 days per week. The number 1.1 is the long-term average or expected value if the men'south soccer team plays soccer week after calendar week after week. We say μ = 1.1.
Detect the expected value of the number of times a newborn baby'south crying wakes its female parent after midnight. The expected value is the expected number of times per calendar week a newborn babe'due south crying wakes its mother after midnight. Calculate the standard deviation of the variable as well.
| x | P(10) | x*P(10) | (x – μ)two ⋅ P(x) |
|---|---|---|---|
| 0 | P(x = 0) = | (0) | (0 – ii.ane)2 ⋅ 0.04 = 0.1764 |
| 1 | P(x = 1) = | (1) | (1 – 2.ane)2 ⋅ 0.22 = 0.2662 |
| ii | P(10 = ii) = | (2) | (two – ii.one)2 ⋅ 0.46 = 0.0046 |
| 3 | P(x = 3) = | (three) | (iii – two.1)2 ⋅ 0.18 = 0.1458 |
| 4 | P(x = 4) = | (iv) | (4 – 2.ane)two ⋅ 0.08 = 0.2888 |
| 5 | P(x = v) = | (5) | (five – 2.1)2 ⋅ 0.02 = 0.1682 |
Add together the values in the third column of the table to find the expected value of X:
μ = Expected Value = ![]() = 2.1
= 2.1
Use μ to consummate the table. The fourth column of this table will provide the values you need to calculate the standard divergence. For each value x, multiply the foursquare of its deviation past its probability. (Each deviation has the format 10 – μ).
Add the values in the fourth cavalcade of the table:
0.1764 + 0.2662 + 0.0046 + 0.1458 + 0.2888 + 0.1682 = 1.05
The standard deviation of X is the foursquare root of this sum: σ = ![]() ≈ 1.0247
≈ 1.0247
The mean, μ, of a discrete probability office is the expected value.
![]()
The standard deviation, Σ, of the PDF is the square root of the variance.
![]()
When all outcomes in the probability distribution are equally probable, these formulas coincide with the mean and standard deviation of the set of possible outcomes.
Suppose yous play a game of chance in which 5 numbers are chosen from 0, 1, ii, 3, 4, 5, 6, 7, 8, 9. A estimator randomly selects five numbers from zero to nine with replacement. You lot pay ?2 to play and could profit ?100,000 if you friction match all five numbers in guild (you become your ?2 back plus ?100,000). Over the long term, what is your expected profit of playing the game?
To exercise this problem, fix an expected value table for the amount of coin you lot tin profit.
Let 10 = the amount of money you profit. The values of x are not 0, 1, 2, three, four, 5, vi, seven, viii, ix. Since you are interested in your profit (or loss), the values of x are 100,000 dollars and −2 dollars.
To win, you must get all five numbers right, in gild. The probability of choosing one correct number is ![]() because at that place are ten numbers. You lot may choose a number more than once. The probability of choosing all 5 numbers correctly and in order is
because at that place are ten numbers. You lot may choose a number more than once. The probability of choosing all 5 numbers correctly and in order is
![]()
Therefore, the probability of winning is 0.00001 and the probability of losing is
![]()
The expected value table is as follows:
| x | P(x) | x*P(x) | |
|---|---|---|---|
| Loss | –ii | 0.99999 | (–2)(0.99999) = –one.99998 |
| Profit | 100,000 | 0.00001 | (100000)(0.00001) = 1 |
Since –0.99998 is almost –1, you would, on boilerplate, expect to lose approximately ?1 for each game y'all play. However, each time you play, y'all either lose ?2 or profit ?100,000. The ?1 is the average or expected LOSS per game after playing this game over and over.
Endeavour It
You are playing a game of chance in which iv cards are drawn from a standard deck of 52 cards. You guess the suit of each card before it is drawn. The cards are replaced in the deck on each draw. Yous pay ?1 to play. If you gauge the right accommodate every fourth dimension, y'all get your coin back and ?256. What is your expected profit of playing the game over the long term?
Suppose you lot play a game with a biased money. You play each game by tossing the coin one time. P(heads) = ![]() and P(tails) =
and P(tails) = ![]() . If you toss a head, you pay ?6. If you lot toss a tail, you win ?10. If you play this game many times, will you come out alee?
. If you toss a head, you pay ?6. If you lot toss a tail, you win ?10. If you play this game many times, will you come out alee?
a. Define a random variable Ten.
b. Complete the following expected value table.
| x | ____ | ____ | |
|---|---|---|---|
| WIN | 10 | | ____ |
| LOSE | ____ | ____ | |
b.
| x | P(10) | xP(x) | |
|---|---|---|---|
| WIN | 10 | | |
| LOSE | –half dozen | | |
c. What is the expected value, μ? Do you come out ahead?
c. Add the concluding cavalcade of the tabular array. The expected value μ = ![]() . Yous lose, on average, well-nigh 67 cents each fourth dimension you play the game and so you practice not come out ahead.
. Yous lose, on average, well-nigh 67 cents each fourth dimension you play the game and so you practice not come out ahead.
Similar data, probability distributions take standard deviations. To summate the standard deviation (σ) of a probability distribution, detect each deviation from its expected value, square it, multiply information technology by its probability, add the products, and take the square root. To understand how to do the calculation, look at the table for the number of days per calendar week a men'south soccer team plays soccer. To detect the standard deviation, add the entries in the cavalcade labeled (x – μ)2 P(10) and take the foursquare root.
| x | P(x) | x*P(x) | (x – μ)2 P(ten) |
|---|---|---|---|
| 0 | 0.2 | (0)(0.2) = 0 | (0 – i.1)2(0.2) = 0.242 |
| one | 0.5 | (i)(0.5) = 0.5 | (1 – one.1)ii(0.five) = 0.005 |
| 2 | 0.3 | (2)(0.3) = 0.6 | (2 – 1.1)two(0.three) = 0.243 |
Add the terminal column in the table. 0.242 + 0.005 + 0.243 = 0.490. The standard deviation is the foursquare root of 0.49, or σ = ![]() = 0.7
= 0.7
By and large for probability distributions, nosotros use a estimator or a computer to summate μ and σ to reduce roundoff error. For some probability distributions, in that location are short-cut formulas for calculating μ and σ.
Toss a fair, six-sided die twice. Let 10 = the number of faces that show an fifty-fifty number. Construct a tabular array like (Figure) and calculate the hateful μ and standard divergence σ of X.
Tossing ane fair six-sided dice twice has the same sample space as tossing ii fair six-sided dice. The sample infinite has 36 outcomes:
| (1, i) | (1, two) | (1, 3) | (i, 4) | (one, five) | (1, 6) |
| (2, 1) | (two, ii) | (2, 3) | (2, 4) | (2, five) | (ii, half dozen) |
| (3, 1) | (3, 2) | (iii, three) | (3, iv) | (3, five) | (3, half dozen) |
| (4, 1) | (iv, 2) | (4, iii) | (4, 4) | (4, 5) | (iv, 6) |
| (5, 1) | (5, two) | (5, 3) | (five, 4) | (v, 5) | (5, 6) |
| (6, i) | (6, 2) | (6, 3) | (half-dozen, four) | (6, v) | (6, half-dozen) |
Employ the sample space to complete the post-obit table:
| x | P(x) | x P(x) | (ten – μ)2 |
|---|---|---|---|
| 0 | | 0 | (0 – 1)2 ⋅ |
| ane | | | (1 – 1)2 ⋅ |
| ii | | | (1 – 1)2 ⋅ |
Add the values in the tertiary cavalcade to discover the expected value: μ = ![]() = i. Utilize this value to consummate the 4th cavalcade.
= i. Utilize this value to consummate the 4th cavalcade.
Add together the values in the fourth column and have the square root of the sum: σ = ![]() ≈ 0.7071.
≈ 0.7071.
On May 11, 2013 at 9:30 PM, the probability that moderate seismic activity (one moderate earthquake) would occur in the side by side 48 hours in Iran was virtually 21.42%. Suppose you lot make a bet that a moderate earthquake will occur in Islamic republic of iran during this flow. If you win the bet, you lot win ?50. If you lose the bet, you lot pay ?20. Let X = the amount of turn a profit from a bet.
P(win) = P(i moderate earthquake volition occur) = 21.42%
P(loss) = P(i moderate earthquake will not occur) = 100% – 21.42%
If you bet many times, will you come out ahead? Explain your answer in a consummate judgement using numbers. What is the standard divergence of X? Construct a table similar to (Figure) and (Figure) to help you answer these questions.
| x | P(ten) | ten (Px) | (10 – μ)2 P(ten) | |
|---|---|---|---|---|
| win | 50 | 0.2142 | 10.71 | [l – (–5.006)]2(0.2142) = 648.0964 |
| loss | –20 | 0.7858 | –15.716 | [–20 – (–five.006)]ii(0.7858) = 176.6636 |
Mean = Expected Value = 10.71 + (–15.716) = –5.006.
If you make this bet many times nether the same conditions, your long term effect will be an average loss of ?5.01 per bet.
![]()
Try It
On May 11, 2013 at 9:30 PM, the probability that moderate seismic activity (one moderate earthquake) would occur in the next 48 hours in Japan was most i.08%. Equally in (Figure), you bet that a moderate convulsion will occur in Japan during this catamenia. If yous win the bet, you win ?100. If you lot lose the bet, you lot pay ?10. Let X = the corporeality of profit from a bet. Find the mean and standard deviation of X.
Some of the more mutual discrete probability functions are binomial, geometric, hypergeometric, and Poisson. Most elementary courses do non cover the geometric, hypergeometric, and Poisson. Your instructor will let you know if he or she wishes to comprehend these distributions.
A probability distribution function is a pattern. Y'all try to fit a probability problem into a pattern or distribution in order to perform the necessary calculations. These distributions are tools to make solving probability problems easier. Each distribution has its ain special characteristics. Learning the characteristics enables you lot to distinguish amongst the different distributions.
Affiliate Review
The expected value, or hateful, of a discrete random variable predicts the long-term results of a statistical experiment that has been repeated many times. The standard deviation of a probability distribution is used to measure the variability of possible outcomes.
Formula Review
Hateful or Expected Value: ![]()
Standard Deviation: ![]()
Complete the expected value tabular array.
| 10 | P(ten) | x*P(10) |
|---|---|---|
| 0 | 0.two | |
| 1 | 0.two | |
| two | 0.4 | |
| iii | 0.two |
<!– <solution id="fs-idm67031296″>
–>
Find the expected value from the expected value tabular array.
| 10 | P(10) | ten*P(10) |
|---|---|---|
| 2 | 0.ane | 2(0.1) = 0.ii |
| iv | 0.three | iv(0.iii) = 1.2 |
| 6 | 0.4 | 6(0.iv) = 2.iv |
| 8 | 0.ii | eight(0.2) = ane.6 |
0.two + one.ii + 2.4 + 1.6 = v.4
Find the standard deviation.
| 10 | P(x) | x*P(10) | (x – μ)2 P(10) |
|---|---|---|---|
| 2 | 0.one | two(0.ane) = 0.ii | (ii–5.4)2(0.ane) = 1.156 |
| 4 | 0.3 | four(0.iii) = ane.2 | (four–5.4)ii(0.3) = 0.588 |
| 6 | 0.4 | half-dozen(0.4) = 2.iv | (6–5.four)2(0.4) = 0.144 |
| viii | 0.two | 8(0.two) = ane.six | (8–v.4)2(0.2) = 1.352 |
<!– <solution id="fs-idm40043568″> σ= i.156+0.588+0.144+1.352 = 3.24 =ane.eight –>
Identify the mistake in the probability distribution table.
| 10 | P(10) | x*P(ten) |
|---|---|---|
| 1 | 0.15 | 0.15 |
| ii | 0.25 | 0.50 |
| iii | 0.thirty | 0.ninety |
| 4 | 0.20 | 0.80 |
| v | 0.xv | 0.75 |
The values of P(ten) do non sum to ane.
Identify the mistake in the probability distribution tabular array.
| x | P(ten) | x*P(10) |
|---|---|---|
| 1 | 0.15 | 0.fifteen |
| 2 | 0.25 | 0.40 |
| 3 | 0.25 | 0.65 |
| 4 | 0.twenty | 0.85 |
| v | 0.xv | one |
<!– <solution id="fs-idp3065552″> The values of xP(x) are not correct. –>
Utilise the following data to answer the next 5 exercises: A physics professor wants to know what per centum of physics majors volition spend the adjacent several years doing postal service-graduate research. He has the following probability distribution.
| ten | P(ten) | ten*P(x) |
|---|---|---|
| 1 | 0.35 | |
| 2 | 0.20 | |
| 3 | 0.fifteen | |
| 4 | ||
| five | 0.10 | |
| half-dozen | 0.05 |
Define the random variable X.
Let X = the number of years a physics major will spend doing post-graduate research.
Define P(ten), or the probability of x.
<!– <solution id="fs-idm55979056″> Let P(x) = the probability that a physics major will practice mail-graduate inquiry for ten years. –>
Discover the probability that a physics major will do mail-graduate research for iv years. P(x = four) = _______
ane – 0.35 – 0.xx – 0.xv – 0.10 – 0.05 = 0.15
Discover the probability that a physics major will practice post-graduate inquiry for at about three years. P(10 ≤ iii) = _______
<!– <solution id="fs-idp5192912″> 0.35 + 0.20 + 0.15 = 0.lxx –>
On average, how many years would you lot expect a physics major to spend doing mail-graduate research?
1(0.35) + 2(0.xx) + 3(0.fifteen) + 4(0.15) + 5(0.ten) + 6(0.05) = 0.35 + 0.forty + 0.45 + 0.60 + 0.50 + 0.30 = 2.6 years
Employ the following data to answer the side by side 7 exercises: A ballet instructor is interested in knowing what percent of each year's course will continue on to the next, so that she tin can program what classes to offering. Over the years, she has established the following probability distribution.
- Permit X = the number of years a student will study ballet with the teacher.
- Permit P(ten) = the probability that a student will report ballet ten years.
Complete (Figure) using the data provided.
| x | P(ten) | x*P(x) |
|---|---|---|
| 1 | 0.10 | |
| 2 | 0.05 | |
| 3 | 0.10 | |
| four | ||
| 5 | 0.30 | |
| six | 0.20 | |
| vii | 0.x |
In words, ascertain the random variable X.
X is the number of years a student studies ballet with the teacher.
P(ten = iv) = _______
<!– <solution id="fs-idp93530752″> 1 – 0.10 – 0.05 – 0.10 – 0.30 – 0.xx – 0.x = 0.15 –>
P(x < 4) = _______
0.10 + 0.05 + 0.10 = 0.25
On average, how many years would yous expect a kid to study ballet with this teacher?
<!– <solution id="fs-idp209095920″> 1(0.10) + 2(0.05) + three(0.10) + 4(0.15) + 5(0.30) + half-dozen(0.xx) + 7(0.ten) = iv.5 years –>
What does the column "P(x)" sum to and why?
The sum of the probabilities sum to one because it is a probability distribution.
What does the column "x*P(x)" sum to and why?
<!– <solution id="fs-idp175794960″> The sum of xP(10) = 4.5; information technology is the mean of the distribution. –>
You lot are playing a game by drawing a card from a standard deck and replacing information technology. If the carte is a face card, y'all win ?30. If information technology is non a face card, you pay ?2. There are 12 confront cards in a deck of 52 cards. What is the expected value of playing the game?
![]()
Y'all are playing a game by cartoon a card from a standard deck and replacing it. If the card is a confront card, you win ?thirty. If it is not a face card, you pay ?2. At that place are 12 face cards in a deck of 52 cards. Should you lot play the game?
<!– <solution id="fs-idm123320016″> Yes, because there is a positive expected value, and the more than you play, the more than probable you are to get closer to the expected value. –>
HOMEWORK
A theater grouping holds a fund-raiser. It sells 100 raffle tickets for ?5 apiece. Suppose you purchase iv tickets. The prize is two passes to a Broadway bear witness, worth a total of ?150.
- What are you interested in hither?
- In words, define the random variable X.
- Listing the values that X may take on.
- Construct a PDF.
- If this fund-raiser is repeated often and y'all always purchase four tickets, what would exist your expected boilerplate winnings per raffle?
<!– <solution id="fs-idp146807296″> I am interested in the average profit or loss. Let X = the return from the raffle Win(💲150) or Lose (💲0)
150( one 100 )+0( 99 100 )−xx=−💲xviii.fifty –>
A game involves selecting a card from a regular 52-carte deck and tossing a money. The coin is a fair coin and is equally likely to state on heads or tails.
- If the menu is a face card, and the coin lands on Heads, y'all win ?6
- If the card is a face card, and the money lands on Tails, y'all win ?2
- If the card is not a face card, you lose ?2, no affair what the coin shows.
- Observe the expected value for this game (expected net gain or loss).
- Explain what your calculations indicate about your long-term average profits and losses on this game.
- Should you play this game to win money?
The variable of interest is X, or the gain or loss, in dollars.
The face up cards jack, queen, and king. There are (3)(4) = 12 confront cards and 52 – 12 = 40 cards that are not face cards.
We first need to construct the probability distribution for X. We utilize the menu and coin events to determine the probability for each outcome, but we use the monetary value of X to determine the expected value.
| Card Event | X net gain/loss | P(X) |
|---|---|---|
| Face Card and Heads | 6 | |
| Face Carte and Tails | 2 | |
| (Not Confront Card) and (H or T) | –2 | |
-
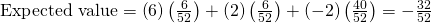
- Expected value = –?0.62, rounded to the nearest cent
- If you lot play this game repeatedly, over a long string of games, you would expect to lose 62 cents per game, on average.
- You lot should not play this game to win coin considering the expected value indicates an expected boilerplate loss.
You buy a lottery ticket to a lottery that costs ?x per ticket. At that place are only 100 tickets available to be sold in this lottery. In this lottery there are one ?500 prize, two ?100 prizes, and iv ?25 prizes. Detect your expected gain or loss.
<!– <solution id="eip-id1170585488797″> Start past writing the probability distribution. Ten is internet gain or loss = prize (if whatever) less 💲ten cost of ticket
Expected Value =(490)( 1 100 )+(90)( two 100 )+(15)( 4 100 )+(−10)( 93 100 )=−💲two. There is an expected loss of 💲2 per ticket, on average. –>
Complete the PDF and respond the questions.
| ten | P(x) | x P(x) |
|---|---|---|
| 0 | 0.iii | |
| ane | 0.two | |
| 2 | ||
| 3 | 0.4 |
- Notice the probability that x = 2.
- Find the expected value.
- 0.1
- i.6
Suppose that you are offered the following "bargain." You scroll a die. If you roll a six, you win ?10. If you curlicue a four or five, you win ?5. If y'all scroll a 1, two, or three, you pay ?half-dozen.
- What are you ultimately interested in here (the value of the coil or the money y'all win)?
- In words, ascertain the Random Variable X.
- List the values that 10 may take on.
- Construct a PDF.
- Over the long run of playing this game, what are your expected boilerplate winnings per game?
- Based on numerical values, should y'all take the deal? Explain your decision in complete sentences.
<!– <solution id="fs-idp133159792″> the coin won X = the amount of money won or lost 💲5, –💲6, 💲x
Expected Value = (10) ane 6 + (five) 2 6 – (6) three 6 = 0.33 Yeah, the expected value is 33 cents –>
A venture capitalist, willing to invest ?1,000,000, has three investments to cull from. The get-go investment, a software company, has a 10% adventure of returning ?5,000,000 profit, a thirty% chance of returning ?1,000,000 turn a profit, and a 60% chance of losing the million dollars. The second company, a hardware company, has a xx% adventure of returning ?three,000,000 turn a profit, a xl% run a risk of returning ?ane,000,000 profit, and a 40% chance of losing the million dollars. The third company, a biotech firm, has a 10% chance of returning ?vi,000,000 profit, a 70% of no profit or loss, and a twenty% chance of losing the million dollars.
- Construct a PDF for each investment.
- Find the expected value for each investment.
- Which is the safest investment? Why do you lot call up so?
- Which is the riskiest investment? Why practice you lot think so?
- Which investment has the highest expected render, on average?
-
Software Company x P(x) v,000,000 0.10 one,000,000 0.30 –1,000,000 0.lx Hardware Visitor x P(x) 3,000,000 0.xx 1,000,000 0.40 –one,000,00 0.xl Biotech Firm ten P(x) half-dozen,00,000 0.x 0 0.70 –one,000,000 0.20 - ?200,000; ?600,000; ?400,000
- third investment because it has the everyman probability of loss
- first investment because information technology has the highest probability of loss
- second investment
Suppose that 20,000 married adults in the United states of america were randomly surveyed as to the number of children they take. The results are compiled and are used as theoretical probabilities. Let 10 = the number of children married people have.
| ten | P(10) | x P(x) |
|---|---|---|
| 0 | 0.10 | |
| i | 0.xx | |
| 2 | 0.thirty | |
| 3 | ||
| four | 0.10 | |
| 5 | 0.05 | |
| 6 (or more) | 0.05 |
- Find the probability that a married adult has three children.
- In words, what does the expected value in this example correspond?
- Find the expected value.
- Is it more likely that a married developed will accept two to three children or four to half dozen children? How do you know?
<!– <solution id="eip-idp44220400″> 0.2 The average number of children married adults accept. 2.35 two of three children –>
Suppose that the PDF for the number of years it takes to earn a Available of Science (B.S.) degree is given as in (Effigy).
| x | P(x) |
|---|---|
| 3 | 0.05 |
| 4 | 0.40 |
| 5 | 0.thirty |
| vi | 0.15 |
| vii | 0.10 |
On average, how many years do you wait it to take for an individual to earn a B.S.?
four.85 years
People visiting video rental stores often rent more than one DVD at a time. The probability distribution for DVD rentals per client at Video To Go is given in the post-obit tabular array. There is a five-video limit per client at this store, and then nobody ever rents more than 5 DVDs.
| x | P(ten) |
|---|---|
| 0 | 0.03 |
| 1 | 0.50 |
| 2 | 0.24 |
| 3 | |
| four | 0.07 |
| five | 0.04 |
- Describe the random variable X in words.
- Observe the probability that a customer rents three DVDs.
- Find the probability that a customer rents at least iv DVDs.
- Find the probability that a client rents at most two DVDs.
Another shop, Entertainment Headquarters, rents DVDs and video games. The probability distribution for DVD rentals per customer at this store is given as follows. They likewise have a five-DVD limit per client.
x P(ten) 0 0.35 1 0.25 2 0.twenty 3 0.10 4 0.05 five 0.05 - At which shop is the expected number of DVDs rented per customer college?
- If Video to Go estimates that they volition have 300 customers next week, how many DVDs do they expect to rent next week? Answer in sentence class.
- If Video to Go expects 300 customers side by side week, and Entertainment HQ projects that they will have 420 customers, for which shop is the expected number of DVD rentals for adjacent week college? Explain.
- Which of the ii video stores experiences more than variation in the number of DVD rentals per customer? How do you know that?
<!– <solution id="fs-idp138954192″> 10 = the number of video rentals per costumer 0.12 0.eleven 0.77 Video To Go (1.82 expected value vs. one.4 for Entertainment Headquarters) The expected number of videos rented to 300 Video To Go customers is 546. The expected number of videos rented to 420 Entertainment Headquarters customers is 588. Amusement Headquarters will rent more videos. The standard deviation for the number of videos rented at Video To Go is 1.1609. The standard deviation for the number of videos rented at Entertainment Headquarters is ane.4293. Amusement Headquarters has more variation. –>
<!–Review Questions??–>
A "friend" offers y'all the post-obit "bargain." For a ?ten fee, you may pick an envelope from a box containing 100 seemingly identical envelopes. However, each envelope contains a coupon for a costless gift.
- Ten of the coupons are for a gratis souvenir worth ?6.
- Eighty of the coupons are for a free souvenir worth ?8.
- Six of the coupons are for a free souvenir worth ?12.
- Four of the coupons are for a free gift worth ?40.
Based upon the financial gain or loss over the long run, should you play the game?
- Yes, I wait to come up out ahead in money.
- No, I wait to come up out behind in coin.
- It doesn't matter. I expect to break fifty-fifty.
b
Florida State University has 14 statistics classes scheduled for its Summer 2013 term. One class has infinite bachelor for 30 students, viii classes have space for 60 students, one course has space for 70 students, and iv classes have infinite for 100 students.
- What is the boilerplate grade size bold each course is filled to chapters?
- Space is available for 980 students. Suppose that each course is filled to capacity and select a statistics pupil at random. Let the random variable 10 equal the size of the pupil'due south class. Define the PDF for 10.
- Find the mean of X.
- Find the standard divergence of Ten.
<!– <solution id="fs-idm42546736″> The average class size is: xxx+8(60)+70+4(100) xiv =lxx P(10=xxx)= 1 fourteen P(x=60)= 8 14 P(10=70)= ane xiv P(x=100)= 4 14 Consummate the following table to find the hateful and standard deviation of X.
Hateful of X= 30 14 + 480 14 + 70 14 + 400 fourteen = 980 fourteen =seventy Standard Deviation of 10= 114.2857+57.1429+0+257.1429 =20.702 –>
In a lottery, there are 250 prizes of ?5, fifty prizes of ?25, and ten prizes of ?100. Assuming that ten,000 tickets are to exist issued and sold, what is a fair price to accuse to break even?
Let X = the corporeality of money to exist won on a ticket. The post-obit table shows the PDF for X.
| x | P(10) |
|---|---|
| 0 | 0.969 |
| 5 | |
| 25 | |
| 100 | |
Calculate the expected value of X.
0(0.969) + 5(0.025) + 25(0.005) + 100(0.001) = 0.35
A off-white price for a ticket is ?0.35. Any price over ?0.35 volition enable the lottery to enhance money.
kirklandoverearrever.blogspot.com
Source: https://opentextbc.ca/introstatopenstax/chapter/mean-or-expected-value-and-standard-deviation/
0 Response to "You Must Know the Mean of an Activity in Order to Determine Its Standard Deviation"
Post a Comment